Mean Surface Temperature

Setup

First, we need to import all the necessary libraries. Some of them are specifically developed to handle the download and plotting of the data and are hosted at the indicators set-up repository in GitHub

Show code cell source Hide code cell source

import warnings
warnings.filterwarnings("ignore")

Show code cell source Hide code cell source

import os.path as op
import sys
import contextlib

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

from myst_nb import glue 

sys.path.append("../../../../indicators_setup")
from ind_setup.plotting_int import plot_timeseries_interactive, fig_int_to_glue
from ind_setup.plotting import plot_bar_probs, fontsize
from ind_setup.tables import get_data_metrics, plot_df_table

sys.path.append("../../../functions")
from data_downloaders import GHCN

from data_downloaders import GHCN, download_oni_index
from ind_setup.plotting_int import plot_oni_index_th
from ind_setup.plotting import plot_bar_probs_ONI, add_oni_cat
import df2img

Define location and variables of interest

country = 'Palau'
vars_interest = ['TMIN', 'TMAX']

Get Data

update_data = False
path_data = "../../../data"
path_figs = "../../../matrix_cc/figures"

Observations from Koror Station

https://www.ncei.noaa.gov/data/global-historical-climatology-network-daily/doc/GHCND_documentation.pdf

The data used for this analysis comes from the GHCN (Global Historical Climatology Network)-Daily database.
This a database that addresses the critical need for historical daily temperature, precipitation, and snow records over global land areas. GHCN-Daily is a composite of climate records from numerous sources that were merged and then subjected to a suite of quality assurance reviews. The archive includes over 40 meteorological elements including temperature daily maximum/minimum, temperature at observation time, precipitation and more.

The next code blocks download the data and postprocess it to generate an easy to use dataframe with all the variables of interest for the analysis.

Show code cell source Hide code cell source

if update_data:
    df_country = GHCN.get_country_code(country)
    print(f'The GHCN code for {country} is {df_country["Code"].values[0]}')

    df_stations = GHCN.download_stations_info()
    df_country_stations = df_stations[df_stations['ID'].str.startswith(df_country.Code.values[0])]
    print(f'There are {df_country_stations.shape[0]} stations in {country}')

Show code cell source Hide code cell source

if update_data:
    GHCND_dir = 'https://www.ncei.noaa.gov/data/global-historical-climatology-network-daily/access/'
    id = 'PSW00040309' # Koror Station
    dict_min = GHCN.extract_dict_data_var(GHCND_dir, 'TMIN', df_country_stations.loc[df_country_stations['ID'] == id])[0][0]
    dict_max = GHCN.extract_dict_data_var(GHCND_dir, 'TMAX', df_country_stations.loc[df_country_stations['ID'] == id])[0][0]
    st_data = pd.concat([dict_min['data'], (dict_max['data'])], axis=1).dropna()
    st_data['diff'] = st_data['TMAX'] - st_data['TMIN']
    st_data['TMEAN'] = (st_data['TMAX'] + st_data['TMIN'])/2
    st_data.to_pickle(op.join(path_data, 'GHCN_surface_temperature.pkl'))
else:
    st_data = pd.read_pickle(op.join(path_data, 'GHCN_surface_temperature.pkl'))

st_data = st_data.resample('Y').mean()
glue("n_years", len(np.unique(st_data.index.year)), display=False)
glue("start_year", st_data.dropna().index[0].year, display=False)
glue("end_year", st_data.dropna().index[-1].year, display=False)

Analysis

Plotting

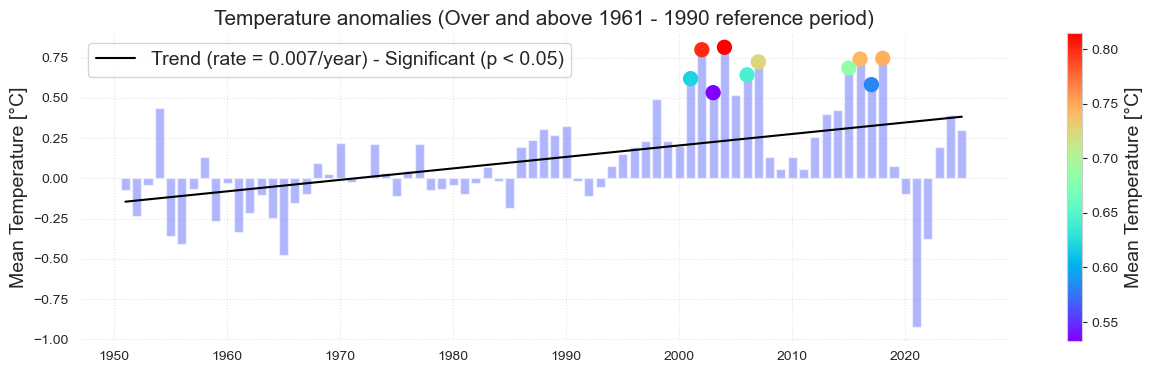
At this piece of code we will plot the Mean annual temperature over time and its associated trend

dict_plot = [{'data' : st_data, 'var' : 'TMEAN', 'ax' : 1, 'label' : 'TMEAN'},
        ]

dict_plot = [{'data' : st_data, 'var' : 'TMEAN', 'ax' : 1, 'label' : 'TMEAN'}]
fig = plot_timeseries_interactive(dict_plot, trendline=True, figsize = (25, 12))

glue("trend_fig_mean", fig_int_to_glue(fig), display=False)

Fig. Annual maxima corresponding to the mean temperature.

fig, ax, trend = plot_bar_probs(x = st_data.index.year, y = st_data['TMEAN'].values , trendline = True,
               figsize = (15, 5), y_label = f'Mean Temperature', return_trend = True)
ax.set_ylim(26, None)

(26.0, 29.842663934426227)

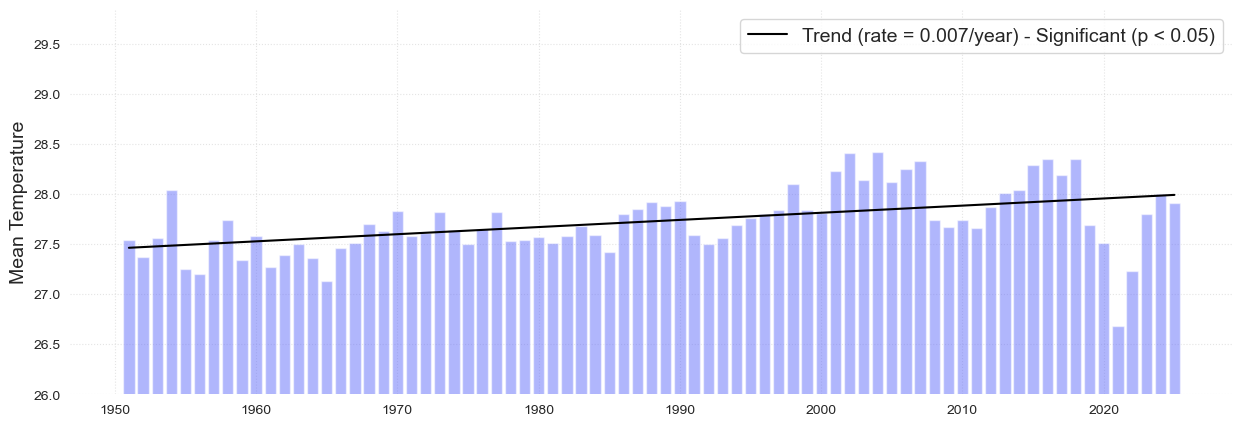
Here we are creating a new column with the information of the temperature refered to the climatology of 1960 to 1990

st_data['TMEAN_ref'] = st_data['TMEAN'] - st_data.loc['1961':'1990'].TMEAN.mean()

import matplotlib.pyplot as plt
plot_bar_probs(x = st_data.index.year, y = st_data.TMEAN_ref, trendline = True, figsize = [15, 4])
plt.title('Temperature anomalies (Over and above 1961 - 1990 reference period)', fontsize = 15);

Table

nevents = 10
top_10 = st_data.sort_values(by='TMEAN_ref', ascending=False).head(nevents)

from ind_setup.tables import plot_df_table

var = 'TMEAN'
df = get_data_metrics(st_data, var, )
fig = plot_df_table(df.T, figsize = (300, 400))

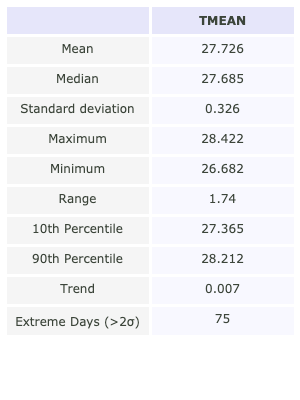
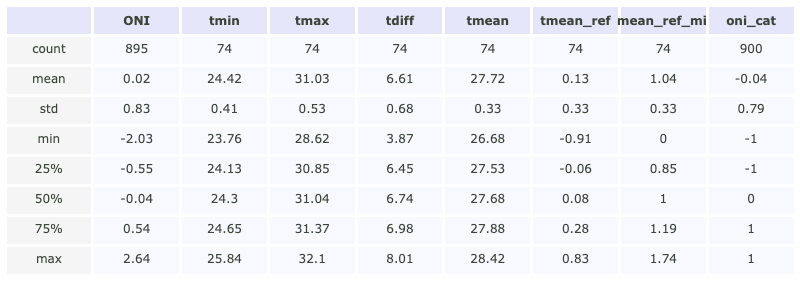
The following bar plot represents the mean temperature anomalies with respect to the 1960-1990 climatology along with the 10 largest temperature events in the record

fig, ax, trend = plot_bar_probs(x=st_data.index.year, y=st_data.TMEAN_ref, trendline=True,
                                y_label='Mean Temperature [°C]', figsize=[15, 4], return_trend=True)

glue("trend_mean", float(trend), display=False)
glue("change_mean", float(trend * len(np.unique(st_data.index.year))), display=False)
glue("top_10_year", float(top_10.sort_index().index.year[0]), display=False)

im = ax.scatter(top_10.index.year, top_10.TMEAN_ref, 
                c=top_10.TMEAN_ref.values, s=100, cmap='rainbow', label='Top 10 warmest years')
plt.title('Temperature anomalies (Over and above 1961 - 1990 reference period)', fontsize=15)
plt.colorbar(im).set_label('Mean Temperature [°C]', fontsize=fontsize)
glue("trend_fig", fig, display=False)

Fig. 1 Annomaly of the mean temperature over and above the 1961-1990 reference period. Overlapping points correspond to the top 10 warmer years.

El Niño Southern Oscillation Analysis

ONI index

The Oceanic Niño Index (ONI) is the standard measure used to monitor El Niño and La Niña events. It is based on sea surface temperature anomalies in the central equatorial Pacific (Niño 3.4 region) averaged over 3-month periods.

https://origin.cpc.ncep.noaa.gov/products/analysis_monitoring/ensostuff/ONI_v5.php

p_data = 'https://psl.noaa.gov/data/correlation/oni.data'

df1 = download_oni_index(p_data)

lims = [-.5, .5]
plot_oni_index_th(df1, lims = lims)

st_data_monthly = st_data.resample('M').mean()
st_data_monthly.index = pd.DatetimeIndex(st_data_monthly.index).to_period('M').to_timestamp() + pd.offsets.MonthBegin(1)

df1['tmin'] = st_data_monthly['TMIN']
df1['tmax'] = st_data_monthly['TMAX']
df1['tdiff'] = df1['tmax'] - df1['tmin']
df1['tmean'] = (df1['tmax'] + df1['tmin'])/2
df1['tmean_ref'] = df1['tmean'] - df1.loc['1961':'1990'].tmean.mean()
df1['tmean_ref_min'] = df1['tmean'] - df1.groupby(df1.index.year).max().tmean.min()
df1 = add_oni_cat(df1, lims = lims)

The following bar plot represents the mean temperature anomalies with respect to the 1960-1990 climatology. The color of the bar represents wether it is a El Niño or La Niña year.

df2 = df1.resample('Y').mean()
fig = plot_bar_probs_ONI(df2, var='tmean_ref');
fig.suptitle('Temperature Anomaly over the 1961-1990 mean', fontsize = fontsize)
plt.savefig(op.join(path_figs, 'F2_ST_Mean.png'), dpi=300, bbox_inches='tight')
plt.close()
# plt.show()

glue("fig_ninho", fig, display=False)

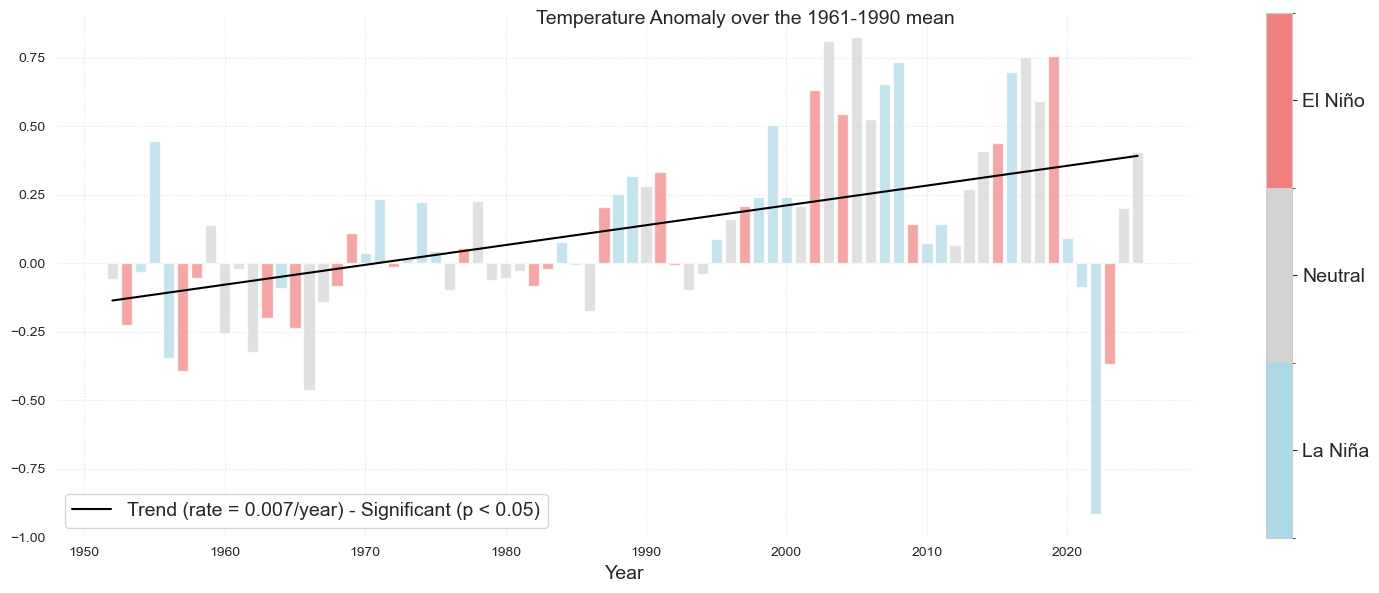
Fig. 2 Annual mean temperature anomalies relative to 1961–1990 climatology at Koror. The solid black line represents the trend, which is statistically significant (p < 0.05). Shading in the bar plots represent El Niño (red), La Niña (blue) and Neutral (grey) phases of ENSO as defined by values of the Oceanic Niño Index (ONI).

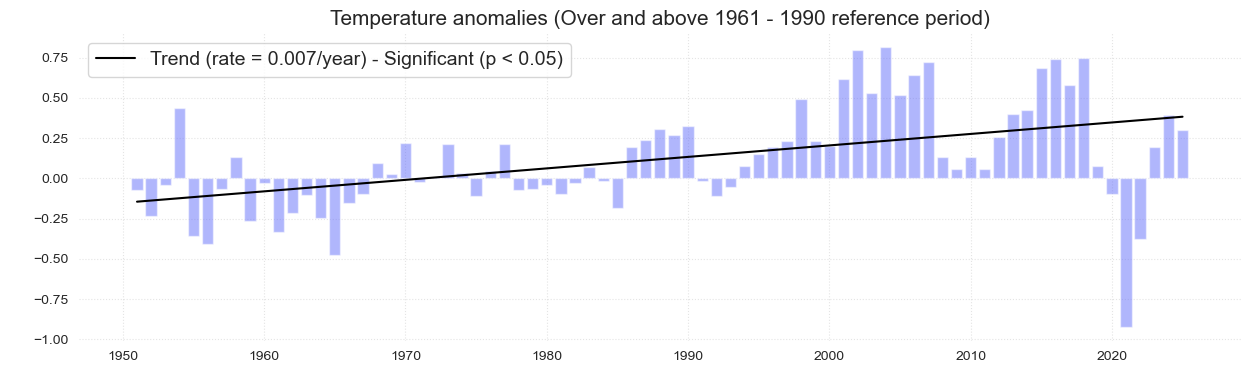
df_format = np.round(df1.describe(), 2)

Generate table

Table sumarizing different metrics of the data analyzed in the plots above

fig = plot_df_table(df_format)
df2img.save_dataframe(fig=fig, filename="getting_started.png")