Minor Flood Frequency and Duration

Minor Flood Frequency and Duration#

../../../_images/3ecabc60085926c638998d4615ba763ff777cfc4d37f22a2700efef97497d710.png

In this notebook we will plot two indicators concerning flooding at the Malakal tide gauge, after first taking a general look at the type of data we are able to plot from the UH Sea Level Center. These indicators are based on a ‘flooding’ threshold, using relative sea level.

Setup#

We first need to import the necessary libraries, access the data, and make a quick plot to ensure we will be analyzing the right thing.

Import necessary libraries.#

# Standard libraries
import os
import os.path as op
import datetime
from pathlib import Path
import sys

# Data manipulation libraries
import numpy as np
import pandas as pd
import xarray as xr

# Data analysis libraries
import scipy.stats as stats

# Visualization libraries
import matplotlib.pyplot as plt
import seaborn as sns
import cartopy.crs as ccrs
import cartopy.feature as cfeature
from matplotlib.colors import Normalize

from urllib.request import urlretrieve #used for downloading files

# Miscellaneous
from myst_nb import glue  # used for figure numbering when exporting to LaTeX

sys.path.append("../../../functions")
from data_downloaders import download_oni_index

Next, we’ll establish our directory for saving and reading data, and our output files.

Caution

You will need to change the variable for “output_dir” to your own output path to save figures and tables to a place of your choosing.

data_dir = Path('../../../data')
path_figs = "../../../matrix_cc/figures"
data_dir = Path(data_dir,'sea_level')

#CHANGE THIS TO YOUR PATH!!
output_dir = Path('/Users/laurac/Library/Mobile Documents/com~apple~CloudDocs/Projects/CC_indicators/CC_indicators/data/')  # EDIT THIS TO YOUR PATH

# Create the output directory if it does not exist
output_dir.mkdir(exist_ok=True)
data_dir.mkdir(exist_ok=True)

Retrieve the Tide Station(s) Data Set(s)#

Next, we’ll access data from the UHSLC. The Malakala tide gauge has the UHSLC ID: 7. We will import the netcdf file into our current data directory, and take a peek at the dataset. We will also import the datums for this location.

and we’ll save a few variables that will come up later for report generation.

Set the Datum to MHHW#

In this example, we will set the datum to MHHW. This can be hard coded, or we can write a script to read in the station datum information from UHSLC, below.

def get_MHHW_uhslc_datums(id, datumname): 
    
    url = 'https://uhslc.soest.hawaii.edu/stations/TIDES_DATUMS/fd/LST/fd'+f'{int(id):03}'+'/datumTable_'+f'{int(id):03}'+'_mm_GMT.csv'
    datumtable = pd.read_csv(url)
    datum = datumtable[datumtable['Name'] == datumname]['Value'].values[0]
    # ensure datum is a float
    datum = float(datum)
    return datum, datumtable

# extract the given datum from the dataframe
datumname = 'MHHW'

datum, datumtable = get_MHHW_uhslc_datums(uhslc_id, datumname)

rsl['datum'] = datum # already in mm
rsl['sea_level_mhhw'] = rsl['sea_level'] - rsl['datum']

# assign units to datum and sea level
rsl['datum'].attrs['units'] = 'mm'
rsl['sea_level_mhhw'].attrs['units'] = 'mm'

glue("datum", datum, display=False)
glue("datumname", datumname, display=False)

datumtable

Show code cell output Hide code cell output

	Name	Value	Description
0	Status	23-Aug-2025	Processing Date
1	Epoch	01-Jan-1983 to 31-Dec-2001	Tidal Datum Analysis Period
2	MHHW	2160	Mean Higher-High Water (mm)
3	MHW	2088	Mean High Water (mm)
4	MTL	1530	Mean Tide Level (mm)
5	MSL	1532	Mean Sea Level (mm)
6	DTL	1457	Mean Diurnal Tide Level (mm)
7	MLW	973	Mean Low Water (mm)
8	MLLW	754	Mean Lower-Low Water (mm)
9	STND	0	Station Datum (mm)
10	GT	1406	Great Diurnal Range (mm)
11	MN	1114	Mean Range of Tide (mm)
12	DHQ	72	Mean Diurnal High Water Inequality (mm)
13	DLQ	219	Mean Diurnal Low Water Inequality (mm)
14	HWI	Unavailable	Greenwich High Water Interval (in hours)
15	LWI	Unavailable	Greenwich Low Water Interval (in hours)
16	Maximum	2785	Highest Observed Water Level (mm)
17	Max Time	23-Jun-2013 22	Highest Observed Water Level Date and Hour (GMT)
18	Minimum	-34	Lowest Observed Water Level (mm)
19	Min Time	19-Jan-1992 16	Lowest Observed Water Level Date and Hour (GMT)
20	HAT	2567	Highest Astronomical Tide (mm)
21	HAT Time	27-Aug-1988 22	HAT Date and Hour (GMT)
22	LAT	175	Lowest Astronomical Tide (mm)
23	LAT Time	31-Dec-1986 16	LAT Date and Hour (GMT)
24	LEV	1644	Switch 1 (mm)
25	LEVB	1541	Switch 2 (mm)

Assess Station Data Quality for the POR (1983-2022)#

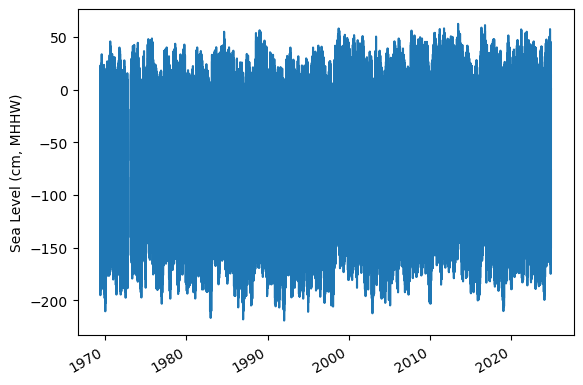
To do this, we’ll plot all the sea level data to make sure our data looks correct, and then we’ll truncate the data set to the time period of record (POR).

fig, ax = plt.subplots(sharex=True)
fig.autofmt_xdate()
ax.plot(rsl.time.values,rsl.sea_level_mhhw.T.values/10)

ax.set_ylabel(f'Sea Level (cm, {datumname})') #divide by 10 to convert to cm

glue("TS_full_fig",fig,display=False)

Identify epoch for the flood frequency analysis#

Now, we’ll calculate trend starting from the beginning of the tidal datum analysis period epoch to the last time processed. The epoch information is given in the datums table.

#get epoch start time from the epoch in the datumtable
epoch_times = datumtable[datumtable['Name'] == 'Epoch']['Value'].values[0]

#parse epoch times into start time
epoch_start = epoch_times.split(' ')[0]
epoch_start = datetime.datetime.strptime(epoch_start, '%d-%b-%Y')

# and for now, end time the processind end time
epoch_end = epoch_times.split(' ')[2]
epoch_end = datetime.datetime.strptime(epoch_end, '%d-%b-%Y')

# last date is rsl['last_rq_date'].values
data_end = rsl['time'].values[-1]
data_end = pd.to_datetime(data_end)

# start the data at year before epoch_start year on May 1st
data_start = pd.Timestamp(year=epoch_start.year-1, month=5, day=1)
data_start = pd.to_datetime(data_start)

# end the data at April 30th of the year of the last data request
data_end = pd.Timestamp(year=data_end.year, month=4, day=30)
data_end = pd.to_datetime(data_end)

hourly_data = rsl.sel(dict(time=slice(data_start, data_end)))
hourly_data

glue("startDataDateTime",data_start.strftime('%Y-%m-%d'), display=False)
glue("endDataDateTime",data_end.strftime('%Y-%m-%d'), display=False)
glue("startEpochDateTime",epoch_start.strftime('%Y-%m-%d'), display=False)
glue("endEpochDateTime",epoch_end.strftime('%Y-%m-%d'), display=False)

and plot the hourly time series

fig, ax = plt.subplots(sharex=True)
fig.autofmt_xdate()
ax.plot(hourly_data.time.values,hourly_data.sea_level_mhhw.T.values/10) #divide by 10 to convert to cm


ax.set_ylabel(f'Sea Level (cm, {datumname})')

glue("TS_epoch_fig",fig,display=False)

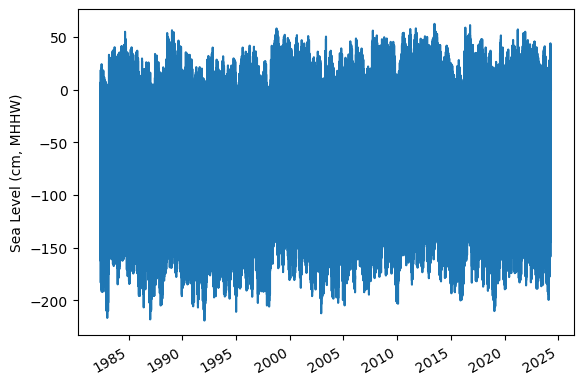
../../../_images/9d2688bc5e7993a562adea9b2127bc7b6ca6346268066ce59942d05d43ee5e2d.png — Fig. 5 Full time series at Malakal,Palau tide gauge for the entire record from 1982-05-01 to 2024-04-30. Note that the sea level is plotted in units of cm, relative to MHHW.#

Assign a Threshold#

The threshold used here to determine a flood event is 30 cm above MHHW.

Note

Change the threshold and see how things change!

threshold = 30 # in cm
glue("threshold",threshold,display=False)

Calculate and Plot Flood Frequency#

To analyze flood frequency, we will look for daily maximum sea levels for each day in our dataset, following and others. Then, we can group our data by year and month to visualize temporal patterns in daily SWL exceedance.

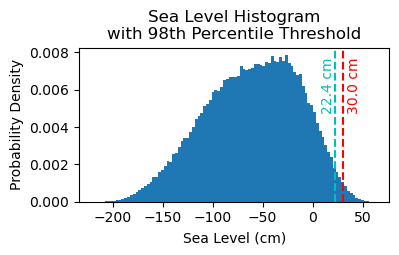
../../../_images/8019736f9485aa295bb61faa3be8379666995fee4d443615f0b610bc8da1c2d2.png — Fig. 6 Histogram of daily maximum water levels at Malakal,Palau tide gauge for the entire record from 1982-05-01 to 2024-04-30, relative to MHHW. The dashed red line indicates the chosen threshold of 30 cm.#

# make a new figure that is 15 x 5
fig, ax = plt.subplots(sharex=True)
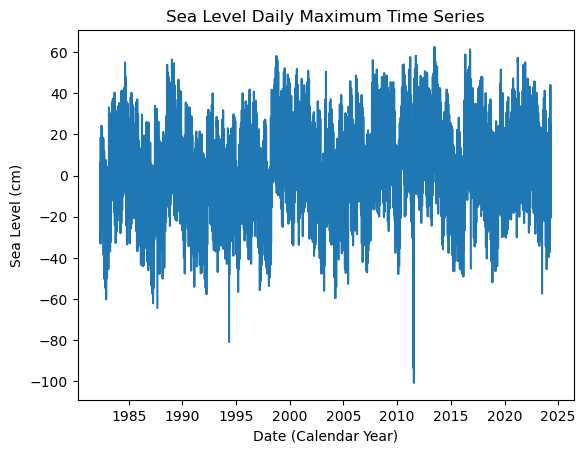
plt.plot(SL_daily_max.time.values, SL_daily_max.sea_level_mhhw.values/10)
plt.xlabel('Date (Calendar Year)')
plt.ylabel('Sea Level (cm)')
plt.title('Sea Level Daily Maximum Time Series')

Text(0.5, 1.0, 'Sea Level Daily Maximum Time Series')

../../../_images/ab65483eb998f89aff08383d94a9bf39881c1d5ac5b080a79c0de19e3ba532a3.png

# Make a pdf of the data with 95th percentile threshold

sea_level_data_cm = hourly_data['sea_level_mhhw'].values/10 # convert to cm
#remove nans
sea_level_data_cm = sea_level_data_cm[~np.isnan(sea_level_data_cm)]

fig, ax = plt.subplots(figsize=(4,2))
ax.hist(sea_level_data_cm, bins=100, density=True, label='Sea Level Data')

#get 95th percentile
threshold98 = np.percentile(sea_level_data_cm, 98)

ax.axvline(threshold, color='r', linestyle='--', label='Threshold: {:.4f} cm'.format(threshold))
ax.axvline(threshold98, color='c', linestyle='--', label='Threshold: {:.4f} cm'.format(threshold98))

ax.set_xlabel('Sea Level (cm)')
ax.set_ylabel('Probability Density')
# make the title two lines
ax.set_title('Sea Level Histogram\nwith 98th Percentile Threshold')

# add label to dashed line
# get value of middle of y-axis for label placement
ymin, ymax = ax.get_ylim()
yrange = ymax - ymin
y_middle = ymin + 0.75*yrange

ax.text(threshold+4, y_middle, '{:.1f} cm'.format(threshold), rotation=90, va='center', ha='left', color='r')
ax.text(threshold98, y_middle, '{:.1f} cm'.format(threshold98), rotation=90, va='center', ha='right', color='c')

glue("histogram_fig", fig, display=False)

# Find all days where sea level exceeds the threshold
flood_days_df = SL_daily_max.to_dataframe().reset_index()

flood_days_df['year_storm'] = flood_days_df['time'].dt.year
flood_days_df.loc[flood_days_df['time'].dt.month > 4, 'year_storm'] = flood_days_df['time'].dt.year + 1

#filter flood hours
flood_days_df = flood_days_df[flood_days_df['sea_level_mhhw'] > threshold*10]

flood_days_per_year = flood_days_df.groupby('year_storm').size().reset_index(name='flood_days_count')

all_years = pd.DataFrame({'year_storm': range(flood_days_df['year_storm'].min(), flood_days_df['year_storm'].max() + 1)})

flood_days_per_year = all_years.merge(flood_days_per_year, on='year_storm', how='left').fillna(0)

flood_days_per_year['flood_days_count'] = flood_days_per_year['flood_days_count'].astype(int)

flood_hours_df = hourly_data.to_dataframe().reset_index()

flood_hours_df['year_storm'] = flood_hours_df['time'].dt.year
flood_hours_df.loc[flood_hours_df['time'].dt.month > 4, 'year_storm'] = flood_hours_df['time'].dt.year + 1

#filter flood hours
flood_hours_df = flood_hours_df[flood_hours_df['sea_level_mhhw'] > threshold*10]

flood_hours_per_year = flood_hours_df.groupby('year_storm').size().reset_index(name='flood_hours_count')

all_years = pd.DataFrame({'year_storm': range(flood_hours_df['year_storm'].min(), flood_hours_df['year_storm'].max() + 1)})

flood_hours_per_year = all_years.merge(flood_hours_per_year, on='year_storm', how='left').fillna(0)

flood_hours_per_year['flood_hours_count'] = flood_hours_per_year['flood_hours_count'].astype(int)

Let’s have a quick look at the data in flood_hours_per_year:

# show the first few rows of the flood_days_per_year dataframe
flood_days_per_year.head()

	year_storm	flood_days_count
0	1983	1
1	1984	33
2	1985	40
3	1986	9
4	1987	0

# add nino
p_data = 'https://psl.noaa.gov/data/correlation/oni.data'
oni = download_oni_index(p_data)

/Users/laurac/Library/Mobile Documents/com~apple~CloudDocs/Projects/CC_indicators/CC_indicators/notebooks_historical/ocean/1_sea_level/../../../functions/data_downloaders.py:242: FutureWarning: The 'delim_whitespace' keyword in pd.read_csv is deprecated and will be removed in a future version. Use ``sep='\s+'`` instead
  oni = pd.read_csv(

# add column for oni values to flood_days_per_year, with average ONI value for the storm year
# first establish storm year for each , given that the date is the index
oni['year_storm'] = oni.index.year

# if the month is less than 5, then the storm year is the year before
oni.loc[oni.index.month > 4, 'year_storm'] = oni.loc[oni.index.month > 4, 'year_storm'] + 1

# group by storm year and get the mean ONI value
oni_year = oni.groupby('year_storm').mean()

# merge the oni values with the flood_days_per_year dataframe
flood_days_per_year = flood_days_per_year.merge(oni_year, on='year_storm', how='left')

def detect_enso_events(oni_df):
    """
    Detects El Niño and La Niña events within a storm year based on the ONI index.
    An El Niño event is defined as having 5 consecutive months with ONI > 0.5.
    A La Niña event is defined as having 5 consecutive months with ONI < -0.5.

    Parameters:
    oni_df (pd.DataFrame): DataFrame containing the ONI index with a datetime index.

    Returns:
    pd.DataFrame: DataFrame with columns 'year_storm' and 'event' indicating the type of event ('El Niño', 'La Niña', or 'Neutral').
    """
    oni_df['event'] = 'Neutral'
    oni_df['year_storm'] = oni_df.index.year
    oni_df.loc[oni_df.index.month > 4, 'year_storm'] += 1

    for year in oni_df['year_storm'].unique():
        yearly_data = oni_df[oni_df['year_storm'] == year]['ONI']
        for i in range(len(yearly_data) - 4):
            if all(yearly_data.iloc[i:i+5] > 0.5):
                oni_df.loc[oni_df['year_storm'] == year, 'event'] = 'El Niño'
                break
            elif all(yearly_data.iloc[i:i+5] < -0.5):
                oni_df.loc[oni_df['year_storm'] == year, 'event'] = 'La Niña'
                break

    return oni_df[['year_storm', 'event']].drop_duplicates().reset_index(drop=True)

# Example usage:
# oni_df = download_oni_index(p_data)  # Assuming this function is already defined and returns a DataFrame with ONI index
enso_events = detect_enso_events(oni)

# show the first few rows of the enso_events dataframe
enso_events.head()

	year_storm	event
0	1951	Neutral
1	1952	El Niño
2	1953	Neutral
3	1954	El Niño
4	1955	La Niña

# add enso events to flood_days_per_year
flood_days_per_year = flood_days_per_year.merge(enso_events, on='year_storm', how='left')
flood_days_per_year.head()

	year_storm	flood_days_count	ONI	event
0	1983	1	1.510833	El Niño
1	1984	33	-0.246667	Neutral
2	1985	40	-0.643333	La Niña
3	1986	9	-0.434167	Neutral
4	1987	0	0.745000	El Niño

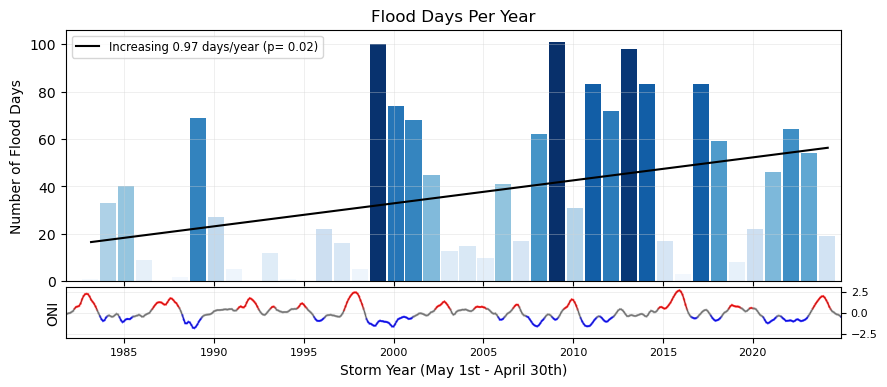
Plot Flood Frequency Counts#

The flood frequency counts are defined as the number of time periods that exceed a given threshold within a year. This plot follows .

# Create two subplots sharing the same x-axis
fig, (ax1, ax2) = plt.subplots(
    2, 1, figsize=(10, 4),  sharex=True, gridspec_kw={"height_ratios": [5, 1],"hspace": 0.04, }
)
# Plot the bar chart for flood days on the first subplot
x_values = flood_days_per_year['year_storm']  # Assuming this is already aligned to storm years
x_values_offset = x_values - 4/12  # Shift x-values to align with the storm years
y_values = flood_days_per_year['flood_days_count']
bar_width = 0.9

flooding_colors = sns.color_palette("Blues", as_cmap=True)
norm = Normalize(vmin=min(y_values), vmax=max(y_values))
colors = flooding_colors(norm(y_values))

ax1.bar(x_values_offset, y_values, width=bar_width, color=colors, align='edge')

ax1.set_ylabel('Number of Flood Days')
ax1.set_title('Flood Days Per Year')
ax1.grid(color='lightgray', linestyle='-', linewidth=0.5, alpha=0.5)

# Plot the ONI index on the second subplot
oni['year_float'] = oni.index.year + (oni.index.month - 1) / 12

# shifted x-axis to align with flood days histogram storm years

# x_offset = flood_days_per_year['year_storm'].min() + 4/12

ax2.plot(oni['year_float'], oni['ONI'], color='k',linewidth=0.5, label='ONI')
ax2.set_ylabel('ONI')
ax2.set_xlabel('Storm Year (May 1st - April 30th)')
ax2.grid(color='lightgray', linestyle='-', linewidth=0.5, alpha=0.5)
ax2.set_ylim(-3, 3)

ax1.set_xlim(x_values_offset.min()-bar_width, x_values.max()+bar_width)
ax2.set_xlim(x_values_offset.min()-bar_width, x_values.max()+bar_width)

# Define thresholds for ONI values
el_nino_threshold = 0.5
la_nina_threshold = -0.5

# Loop through the data to plot segments with different colors
for i in range(len(oni) - 1):
    x = oni['year_float'].iloc[i:i+2]
    y = oni['ONI'].iloc[i:i+2]
    
    if y.mean() >= el_nino_threshold:
        color = 'red'
    elif y.mean() <= la_nina_threshold:
        color = 'blue'
    else:
        color = 'gray'
    
    ax2.plot(x, y, color=color, linewidth=1.5, alpha=0.5)




# put y-axis labels on the right side for ax2
ax2.yaxis.tick_right()

# set font size for tick labels
ax2.tick_params(axis='both', which='major', labelsize=8)

# Add the trendline to the first subplot

# Aggregating data and fitting the trendline

slope, intercept, r_value, p_value, std_err = stats.linregress(x_values_offset+0.5, y_values)
trendDays = intercept + slope * (x_values_offset+0.5)
trendLabel = 'Increasing {:.2f} days/year (p= {:.2f})'.format(slope,p_value)

if p_value < 0.05:
    linestyleTrend = '-'
else:
    linestyleTrend = '--'

ax1.plot(x_values_offset+0.5, trendDays, color='black', linestyle=linestyleTrend, label=trendLabel)

# Adding the legend
ax1.legend(loc='upper left', fontsize='small')

# # save the trendline values
glue("day_per_year_trend",slope,display=False)
glue("p_value_days",p_value,display=False)

# # save the figure
glue("fig-threshold_counts_enso", fig, display=False)

# save to output directory
fig.savefig(output_dir / "SL_FloodFrequency_threshold_counts_days.png", dpi=300, bbox_inches='tight')

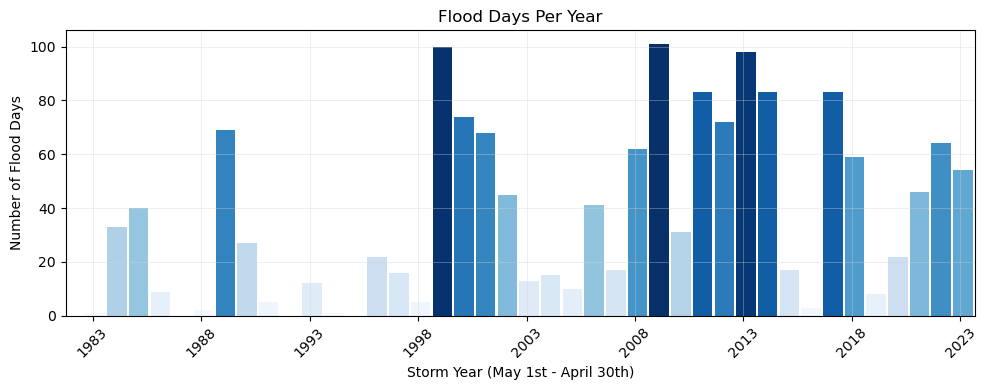
Here is a more simplified plot of the same thing.

x_values = flood_days_per_year['year_storm']  # Assuming this is already aligned to storm years
y_values = flood_days_per_year['flood_days_count']
bar_width = 0.9  # Adjust the width of the bars

# Offset x-values by 4/12 (4 months = May start)
x_values_offset = x_values - 4/12

# Plot the bar chart
fig, ax = plt.subplots(figsize=(10, 4))
ax.bar(x_values_offset, y_values, width=bar_width, color=colors, align='edge')

# Add gridlines for better readability
ax.grid(color='lightgray', linestyle='-', linewidth=0.5, alpha=0.5)

# Add labels and title
ax.set_xlabel('Storm Year (May 1st - April 30th)')
ax.set_ylabel('Number of Flood Days')
ax.set_title('Flood Days Per Year')

# Adjust x-ticks to match storm years
ax.set_xticks(x_values[::5])  # Use storm years for ticks, spaced every 5 years
ax.set_xticklabels(x_values[::5].astype(int), rotation=45)

# Set x-limits to ensure all bars are visible
ax.set_xlim(x_values_offset.min() - bar_width, x_values_offset.max())

# Show the plot
plt.tight_layout()
plt.show()

../../../_images/770028e1f6dc708dfde66e445ff95606c090b11fe2a25bd86ca95a15625e29d6.png

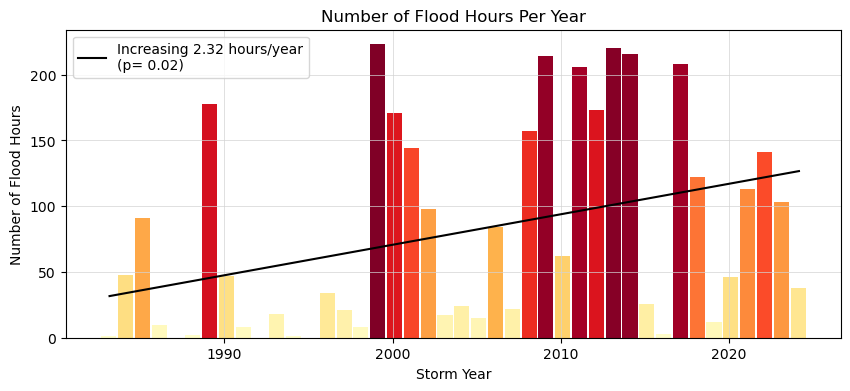
Plot Flood Duration#

This next plot examines the average duration of flooding events as defined by the threshold. Note that in this calculation these hours need not be continuous (and thus any changes in the scale of the flooding in terms of time-extent is not readily apparent, only the yearly summation.)

# Adjusting the heatmap palette to improve readability
from matplotlib.colors import Normalize

adjusted_heatmap_palette = sns.color_palette("YlOrRd", as_cmap=True)



# Plot the bar chart
fig, ax = plt.subplots(figsize=(10, 4))
# Adding a light gray grid
ax.grid(color='lightgray', linestyle='-', linewidth=0.5)

y_values = flood_hours_per_year['flood_hours_count']
x_values = flood_hours_per_year['year_storm']
bar_width = 0.9
norm = Normalize(vmin=min(y_values), vmax=max(y_values))
colors = adjusted_heatmap_palette(norm(y_values))

# Offset x-values by 4/12 (4 months = May start)
x_values_offset = x_values - 4/12

ax.bar(x_values_offset, y_values, width=bar_width, color=colors, align='edge')

ax.set_xlabel('Storm Year')
ax.set_ylabel('Number of Flood Hours')
ax.set_title('Number of Flood Hours Per Year')

slope, intercept, r_value, p_value, std_err = stats.linregress(x_values_offset+0.5, y_values)
trendHours = intercept + slope * (x_values_offset+0.5)
trendLabel = 'Increasing {:.2f} hours/year\n(p= {:.2f})'.format(slope, p_value)

if p_value < 0.05:
    linestyleTrend = '-'
else:
    linestyleTrend = '--'

ax.plot(x_values_offset+0.5, trendHours, color='black', linestyle=linestyleTrend, label=trendLabel)

# Adding the legend
ax.legend(loc='upper left', fontsize='small')

# # save the trendline values
# glue("hours_per_year_trend",slope,display=False)
# glue("p_value_hours",p_value,display=False)

# Adding the legend
ax.legend(loc='upper left')

# glue("duration_fig", fig, display=False)

# save the figure
fig.savefig(output_dir / 'SL_FloodFrequency_threshold_counts_hours.png', bbox_inches='tight')

Calculate the percent change over time#

Next we’ll calculate the percent change over the POR at the tide station/s, for both Frequency and Duration.

The next code cell fits a trend line to the flood days per year data and calculates the trend line. It then plots the data and the trend line in a figure, and calculates the percent change in flood days per year using the trend line. The same process is repeated for flood hours per year.

Now we’ll generate a table with this information, which will be saved as a .csv in the output directory specified at the top of this notebook.

# Calculate the total number of days/hours exceeding the threshold
total_flood_days = flood_days_per_year['flood_days_count'].sum()
total_flood_hours = flood_hours_per_year['flood_hours_count'].sum()

# Calculate the average number of flood days and hours per year
average_flood_days_per_year = total_flood_days / len(flood_days_per_year)
average_flood_hours_per_year = flood_hours_per_year['flood_hours_count'].mean()

# Find the maximum number of flood days in a single year
max_flood_days = flood_days_per_year['flood_days_count'].max()
max_flood_days_year = flood_days_per_year.loc[flood_days_per_year['flood_days_count'].idxmax(), 'year_storm']

# Find the maximum number of flood hours in a single year
max_flood_hours = flood_hours_per_year['flood_hours_count'].max()
max_flood_hours_year = flood_hours_per_year.loc[flood_hours_per_year['flood_hours_count'].idxmax(), 'year_storm']

# calculate the absolute percent change over the entire period using the first and last part of the trend
percent_change_days = (trendDays.iloc[-1]-trendDays.iloc[0])/trendDays.iloc[0]*100
percent_change_hours = (trendHours.iloc[-1]-trendHours.iloc[0])/trendHours.iloc[0]*100

# Create a dataframe for statistics
summary_stats = [
    ('Total Flood Days', int(total_flood_days)),
    ('Average Flood Days per Year', int(average_flood_days_per_year)),
    ('Max Flood Days in a Single Year', int(max_flood_days)),
    ('Year of Max Flood Days', int(max_flood_days_year)),
    ('Total Flood Hours', int(total_flood_hours)),
    ('Average Flood Hours per Year', int(average_flood_hours_per_year)),
    ('Max Flood Hours in a Single Year', int(max_flood_hours)),
    ('Year of Max Flood Hours', int(max_flood_hours_year)),
    ('Percent Change in Flood Days', int(percent_change_days)),
    ('Percent Change in Flood Hours', int(percent_change_hours))
]

# Convert the list of tuples to a pandas DataFrame
summary_stats_df = pd.DataFrame(summary_stats, columns=['Statistic', 'Value'])

# Display the DataFrame
summary_stats_df

	Statistic	Value
0	Total Flood Days	1530
1	Average Flood Days per Year	36
2	Max Flood Days in a Single Year	101
3	Year of Max Flood Days	2009
4	Total Flood Hours	3325
5	Average Flood Hours per Year	79
6	Max Flood Hours in a Single Year	223
7	Year of Max Flood Hours	1999
8	Percent Change in Flood Days	239
9	Percent Change in Flood Hours	300

Create a sub-annual table#

Here we’ll turn our ‘flooding days’ into a dataframe to look at monthly changes through time.

Show code cell source Hide code cell source

import calendar
# Make a dataframe with years as rows and months as columns
df = SL_daily_max.to_dataframe().reset_index()
df['flood_day'] = df['sea_level_mhhw'] > threshold*10

# keep only the flood day and time columns
df = df[['time', 'flood_day']]

df['year'] = df['time'].dt.year
df['month'] = df['time'].dt.month

# adjust for storm year
df.loc[df['month'] > 4, 'year'] = df.loc[df['month'] > 4, 'year'] + 1

# drop original time column
df = df.drop(columns=['time'])

# sum the number of flood days in each month for each storm year
df = df.groupby(['year', 'month']).sum()

# pivot the table
df = df.pivot_table(index='year', columns='month', values='flood_day')

# remove first and last rows (partial years)
# df = df.iloc[1:-1]

# rename year to Storm Year
df.index.name = 'Storm Year'

#define reordered months (for storm year, May to April)
month_order = [5,6,7,8,9,10,11,12,1,2,3,4]
month_names = [calendar.month_abbr[i] for i in month_order]
# rename months to month names
df = df[month_order]
df.columns = month_names

# add a column for the total number of flood days in each year
df['Annual'] = df.sum(axis=1)



# add a row for the total number of flood days in each month, normalized the total flood days (last row, last column)
df.loc['Monthly Total (%)'] = df.sum()
df.loc['Monthly Total (%)'] = 100*df.loc['Monthly Total (%)']/df.loc['Monthly Total (%)', 'Annual']

station_name = SL_daily_max['station_name'].values[0].decode('utf-8') +', ' + SL_daily_max['station_country'].values[0].decode('utf-8')

tableTitle = station_name + ': Days Exceeding ' + str(threshold) + ' cm above MHHW'
# Apply background gradient and add a title with larger text
styled_df = df.style.background_gradient(
    cmap='Purples', axis=None, subset=(df.index[:-1], df.columns[:-1])
).format("{:.0f}").background_gradient(
    cmap='Grays', axis=None, subset=(df.index[-1], df.columns[:-1])
).format("{:.0f}").set_caption(tableTitle).set_table_styles([
    {
        'selector': 'caption',
        'props': [('font-size', '16px'), ('margin-bottom', '10px')]
    }
])

styled_df

Malakal, Palau: Days Exceeding 30 cm above MHHW
	May	Jun	Jul	Aug	Sep	Oct	Nov	Dec	Jan	Feb	Mar	Apr	Annual
Storm Year
1983	0	0	0	0	0	0	0	0	0	1	0	0	1
1984	1	5	5	4	3	2	1	0	2	3	1	6	33
1985	5	1	4	9	6	3	4	0	0	0	3	5	40
1986	3	2	0	0	2	2	0	0	0	0	0	0	9
1987	0	0	0	0	0	0	0	0	0	0	0	0	0
1988	0	1	0	1	0	0	0	0	0	0	0	0	2
1989	0	0	4	8	6	7	4	3	17	7	7	6	69
1990	4	0	2	6	5	4	4	0	0	0	0	2	27
1991	3	1	0	0	1	0	0	0	0	0	0	0	5
1992	0	0	0	0	0	0	0	0	0	0	0	0	0
1993	1	2	0	1	3	5	0	0	0	0	0	0	12
1994	0	0	0	0	0	1	0	0	0	0	0	0	1
1995	0	0	0	0	0	0	0	0	0	0	0	0	0
1996	0	0	1	3	0	2	4	0	0	1	0	11	22
1997	0	0	2	5	3	4	2	0	0	0	0	0	16
1998	0	0	0	0	0	0	0	0	0	0	0	5	5
1999	6	5	12	13	12	13	7	6	11	5	7	3	100
2000	5	7	14	11	10	10	6	4	3	4	0	0	74
2001	1	1	8	15	12	7	3	0	1	5	4	11	68
2002	10	7	6	6	6	5	4	0	0	0	1	0	45
2003	0	0	0	5	2	1	0	0	0	0	0	5	13
2004	6	0	0	1	4	2	2	0	0	0	0	0	15
2005	0	0	0	3	0	4	2	0	0	0	1	0	10
2006	0	2	0	6	10	4	0	0	0	2	12	5	41
2007	5	0	3	2	3	4	0	0	0	0	0	0	17
2008	0	0	0	5	11	7	5	4	2	16	7	5	62
2009	7	7	12	15	16	8	6	6	5	7	4	8	101
2010	7	6	5	5	7	1	0	0	0	0	0	0	31
2011	6	6	8	10	6	5	9	7	4	8	9	5	83
2012	0	0	4	13	11	9	7	6	5	4	8	5	72
2013	5	7	17	18	11	7	4	4	5	4	7	9	98
2014	8	15	10	9	14	9	6	5	6	1	0	0	83
2015	1	0	4	5	4	3	0	0	0	0	0	0	17
2016	0	0	0	0	0	0	0	0	0	0	0	3	3
2017	11	9	9	15	13	12	3	4	5	1	0	1	83
2018	4	3	3	4	10	13	8	6	0	2	5	1	59
2019	0	0	2	3	3	0	0	0	0	0	0	0	8
2020	0	0	1	8	5	4	0	0	0	0	1	3	22
2021	3	0	0	1	7	7	4	5	2	0	7	10	46
2022	3	2	0	1	9	8	9	6	3	4	16	3	64
2023	6	5	3	4	11	13	5	3	3	1	0	0	54
2024	0	0	0	4	6	3	0	0	0	0	0	6	19
Monthly Total (%)	7	6	9	14	15	12	7	5	5	5	7	8	100

We can also make a nice plot for printed reports.

---------------------------------------------------------------------------
ModuleNotFoundError                       Traceback (most recent call last)
Cell In[27], line 2
      1 #make a pretty pdf of the table with great_tables
----> 2 from great_tables import GT,html
      4 dfGT = df.copy()
      5 dfGT['Storm Year'] = df.index

ModuleNotFoundError: No module named 'great_tables'

# Define the decades for analysis
decades = [(1983, 1993), (1993, 2003), (2003, 2013), (2013, 2023)]

# Initialize lists to store results
total_flood_days_list = []
average_flood_days_per_year_list = []
percent_increase_days_per_year_list = [0]  # First decade has no previous data for comparison

# Calculate statistics for each decade
for i, (start_year, end_year) in enumerate(decades):
    # Filter the dataframe for the current decade
    flood_days_decade = flood_days_per_year[(flood_days_per_year['year_storm'] >= start_year) & (flood_days_per_year['year_storm'] <= end_year)]
    sum_flood_days_decade = flood_days_decade['flood_days_count'].sum()
    avg_flood_days_decade = sum_flood_days_decade / len(flood_days_decade)
    
    # Append results to lists
    total_flood_days_list.append(sum_flood_days_decade)
    average_flood_days_per_year_list.append(np.round(avg_flood_days_decade,0))
    
    # Calculate percent increase for subsequent decades
    if i > 0:
        prev_avg_flood_days = average_flood_days_per_year_list[0]
        percent_increase = np.round((avg_flood_days_decade - prev_avg_flood_days) / prev_avg_flood_days * 100, 1)
        percent_increase_days_per_year_list.append(percent_increase)

# Create a dataframe for decadal statistics
decadal_stats = pd.DataFrame({
    'decade': ['1983-1993', '1993-2003', '2003-2013', '2013-2023'],
    'total_flood_days': total_flood_days_list,
    'average_flood_days_per_year': average_flood_days_per_year_list,
    'percent_increase_days_per_year': percent_increase_days_per_year_list
})

decadal_stats

	decade	total_flood_days	average_flood_days_per_year	percent_increase_days_per_year
0	1983-1993	194	18.0	0.0
1	1993-2003	350	32.0	76.8
2	2003-2013	524	48.0	164.6
3	2013-2023	528	48.0	166.7

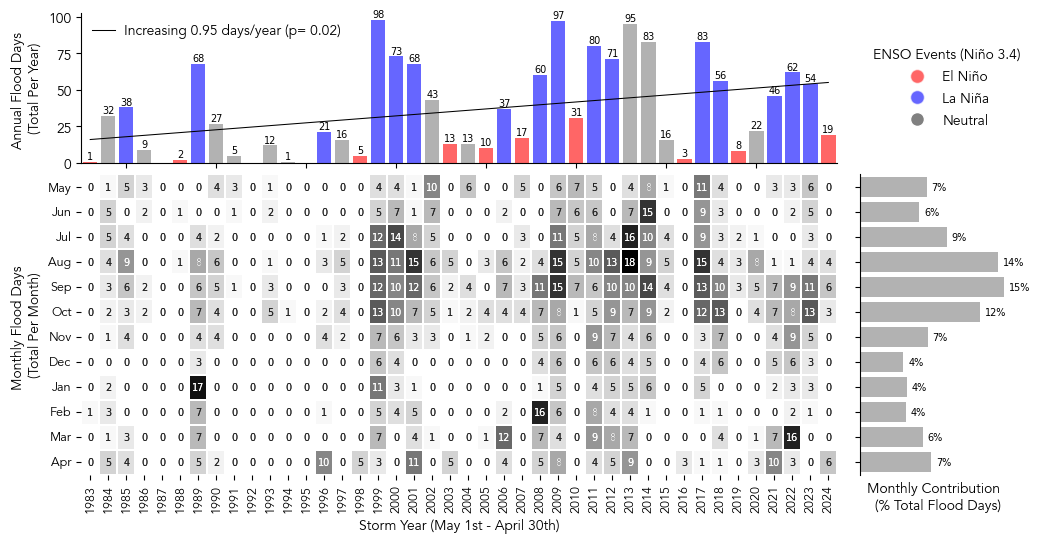
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd


# Create a figure and shared axis layout
fig, axs = plt.subplots(2,2,figsize=(12,6), gridspec_kw={"height_ratios": [1, 2], "hspace": 0.05, "width_ratios":[5,1], "wspace": 0.05})

# put stuff in the figure
# Create heatmap on the left
sns.heatmap(df.iloc[:-1, :-1].T, cmap="Blues", annot=True, fmt=".0f", linewidths=0.2,
            ax=axs[1,0],cbar=False, annot_kws={"size": 7})

# heatmap
sns.heatmap(df.iloc[:-1, :-1].T, cmap="Grays", annot=True, fmt=".0f", linewidths=0.2, 
            ax=axs[1,0],cbar=False, annot_kws={"size": 7})
axs[1,0].set_ylabel("Monthly Flood Days \n(Total Per Month)")
axs[1,0].set_xlabel("Storm Year (May 1st - April 30th)")
axs[1,0].tick_params(axis='y', labelsize=9)
axs[1,0].tick_params(axis='x', labelsize=9)

# map oni_year to colors using enso (we will keep this for now for possible future use)
# oni_colors = ['red' if val > 0.5 else 'blue' if val < -0.5 else 'gray' for val in flood_days_per_year['ONI']]

# color by enso_event
enso_colors = ['red' if val == 'El Niño' else 'blue' if val == 'La Niña' else 'gray' for val in flood_days_per_year['event']]



# yearly totals
ax2 = axs[0,0]
# set ax2 x-axis to be the same as ax1
bars = ax2.bar(df.index[0:-1], df["Annual"][0:-1], color=enso_colors, alpha=0.6, label="Annual Flood Days")
ax2.set_xlim(df.index[0]-0.5, df.index[-2]+0.5)
ax2.set_ylabel("Annual Flood Days \n(Total Per Year)")

# Add annotations to bars
for bar in bars:
    height = bar.get_height()
    if height > 0:
        ax2.text(bar.get_x() + bar.get_width() / 2, height + 0.5, f"{int(height)}", 
                 ha='center', va='bottom', fontsize=7, color="black")

# remove top and right boudaries
ax2.spines['top'].set_visible(False)
ax2.spines['right'].set_visible(False)



# bar plot of monthly totals
ax3 = axs[1,1]
barMonth = ax3.barh(range(1, 13), df.iloc[-1, :-1][::-1], color="gray", alpha=0.6, label="Mean Yearly Flood Days")
ax3.set_yticks(range(1, 13))
ax3.set_ylim(0.5, 12.5)
# remove y-axis labels
ax3.set_yticklabels([])

#remove x-axis ticks and labels
ax3.set_xticks([])

ax3.set_xlabel("Monthly Contribution \n (% Total Flood Days)")

#remove top and right boudaries
for spine in ax3.spines.values():
    spine.set_visible(False)

ax3.spines['left'].set_visible(True)


# add annotations to bars
for bar in barMonth:
    width = bar.get_width()
    if width > 0:
        ax3.text(width + 0.5, bar.get_y() + bar.get_height() / 2, f"{int(width)}%", 
                 ha='left', va='center', fontsize=7, color="black")
        
# ax[0,1] defines the oni_color legend
ax4 = axs[0,1]
ax4.axis('off')
# create a legend for the oni_colors
legend_elements = [plt.Line2D([0], [0], marker='o', color='w', label='El Niño', markerfacecolor='red', markersize=10, alpha=0.6),
                   plt.Line2D([0], [0], marker='o', color='w', label='La Niña', markerfacecolor='blue', markersize=10, alpha=0.6),
                   plt.Line2D([0], [0], marker='o', color='w', label='Neutral', markerfacecolor='gray', markersize=10)]
legend = ax4.legend(handles=legend_elements, loc='center left', title='ENSO Events (Niño 3.4)', frameon=False)


legend_title = legend.get_title()
legend_title.set_fontsize('10')
legend_title.set_fontname('Avenir')
legend_texts = legend.get_texts()
for text in legend_texts:
    text.set_fontname('Avenir')
    text.set_fontsize('10')


# add trendline to the yearly totals
x = df.index[0:-1].astype(int).values
y = df["Annual"][0:-1].values
slope, intercept, r_value, p_value, std_err = stats.linregress(x,y)
trendDays = intercept + slope * x
trendLabel = 'Increasing {:.2f} days/year (p= {:.2f})'.format(slope,p_value)

if p_value < 0.05:
    linestyleTrend = '-'
else:
    linestyleTrend = '--'

ax2.plot(x, trendDays, color='black', linestyle=linestyleTrend, label=trendLabel, linewidth=0.75)

# add another legend for the trendline
# Add a new legend only for the trendline
legendTrend = ax2.legend([plt.Line2D([0], [0], color='black', linestyle=linestyleTrend, linewidth=0.75)],
           [trendLabel], loc='upper left', fontsize='small', frameon=False)
legendTrend_texts = legendTrend.get_texts()
for text in legendTrend_texts:
    text.set_fontname('Avenir')
    text.set_fontsize('10')




# set all fonts in the figure to Avenir
# Iterate over all axes in the figure
for ax in axs.flat:
    # Change font for title, axis labels, and tick labels
    for item in ([ax.title, ax.xaxis.label, ax.yaxis.label] +
                 ax.get_xticklabels() + ax.get_yticklabels()):
        item.set_fontname('Avenir')


#save the figure
fig.savefig(output_dir / 'SL_FloodFrequency_threshold_counts_heatmap.png', bbox_inches='tight')
plt.savefig(op.join(path_figs, 'F11_Minor_flood_matrix.png'), dpi=300, bbox_inches='tight')

../../../_images/7239d2e4ed0291ad3f5b13cc4722939a424dc0fcfe73655c8daf44e86ec32804.png

Create a map#

In this next section we’ll create a map with an icon depicting the percent change over the Period of Record at the tide station/s, for both Frequency and Duration.

The following cell defines a function to add arrow icons denoting percent change.

And here is our final plotting code:

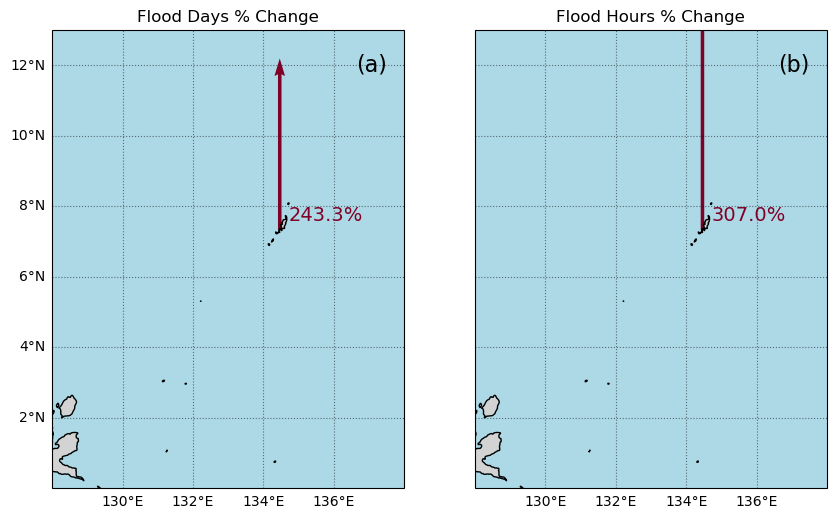
../../../_images/d8efdbc913b5dbd572b2de737d36465ec5a91393683191e533123cdf46a4916b.png